Lavorare su Media ed errore con i dati di LHC

ESPERIENZE DI CLASSE | Matematica, Fisica
La scoperta del bosone di Higgs e l’attenzione mediatica che ne è conseguita hanno reso la fisica delle particelle un argomento di diffuso interesse, tale da affascinare persone di ogni età. In questa scheda propongo un’attività didattica per introdurre i concetti di media e di errore assoluto e relativo proprio partendo da questo ambito di ricerca.
L’attività – rivolta in particolare ad alunni del primo anno di scuola secondaria di secondo grado – si basa sull’utilizzo del sito Hypatia, che permette di lavorare con dati originali provenienti dal Cern. Con essa si intende collegare le conoscenze di base della fisica con le più attuali scoperte scientifiche, con l’obiettivo di affascinare gli alunni introducendoli “in punta di piedi” al mondo degli acceleratori di particelle.
Breve introduzione teorica
Situato tra la Svizzera e la Francia, il Large Hadron Collider (LHC) del Cern costituisce il più grande laboratorio al mondo di fisica delle particelle. Qui gli scienziati cercano di esplorare i segreti della materia e di ricreare ciò che è avvenuto pochi istanti dopo la nascita dell’Universo. Per fare ciò, le particelle sono portate a velocità estremamente elevate (quasi 300 000 000 m/s) e fatte urtare tra di loro. Durante le collisioni si creano nuove particelle, che a loro volta decadono, cioè si trasformano, in altre. Studiando le caratteristiche delle particelle frutto del decadimento è possibile comprendere le proprietà di quelle iniziali.
Per rintracciare le particelle prodotte in seguito alla collisione, si utilizzano strumenti detti rivelatori di particelle: Atlas è uno di essi. È costituito da diversi elementi, ognuno dei quali reagisce in modo differente al passaggio di particelle di diversa natura.
Tra le varie particelle studiate al Cern c’è il bosone Z. Molto comune in condizioni estreme, come nelle esplosioni di supernovae, o alle origini del nostro Universo, esso è una particella neutra con un tempo di vita estremamente breve (3x10-25 s). Questo significa che, pochi istanti dopo essere stato creato, ad esempio dall’urto tra due protoni, decade. In particolare, un bosone Z può decadere in due muoni. Il muone è una particella che interagisce poco con la materia: una volta creato, prosegue pressoché indisturbato la sua traiettoria, essendo in grado di attraversare i materiali di cui è fatto il rivelatore. Poiché studiando le caratteristiche delle particelle prodotte in un decadimento è possibile conoscere proprietà fondamentali della particella iniziale, dallo studio dei muoni è possibile ricavare la massa del bosone Z. L’obiettivo dell’attività proposta è proprio quello di ricavare la massa del bosone Z.
Ricavare la massa del bosone Z: procedimento
1. Per svolgere questo esercizio, per prima cosa è necessario collegarsi al sito Hypatia, per analizzare i dati forniti dal Cern. Dopo aver selezionato la voce Hypatia 4, si accede a una schermata dove sono rintracciabili i seguenti elementi:
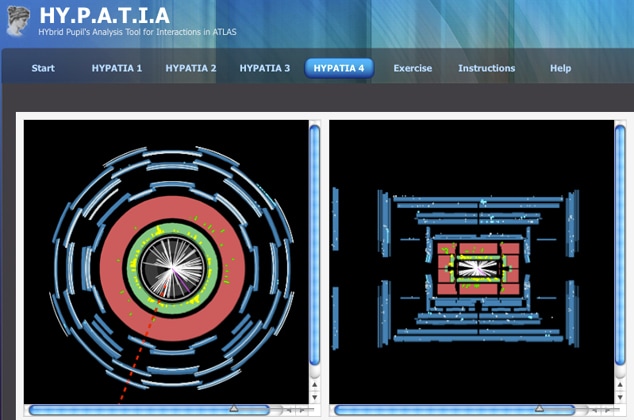
a. Visione trasversale e longitudinale del rivelatore di particelle Atlas. Le zone colorate in modo differente (grigio, verde, rosso, blu) corrispondono ai diversi elementi del rivelatore, in grado di rintracciare particelle differenti. Le righe bianche centrali corrispondono a tracce di particelle che sono state visualizzate nella parte più interna.
b. Il selezionatore di eventi, inizialmente impostato per visualizzare i dati relativi al gruppo 1, evento (ovvero urto) 1.
c. Una tabella che riporta i dati riguardanti le diverse tracce (ovvero le diverse particelle prodotte in seguito alla collisione). Quella che è importante per lo svolgimento di questo esercizio è la prima colonna, che indica se la particella considerata è carica positivamente o negativamente. Infatti, poiché il bosone Z è una particella neutra, dovrà decadere in due muoni, di cui uno positivo, l’altro negativo.
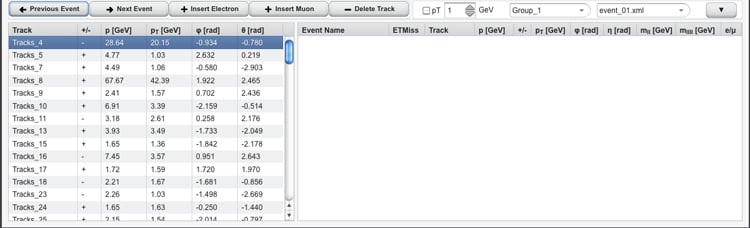
2. Ecco i passaggi per ottenere una stima della massa del bosone Z.
a. Utilizzando il selezionatore di eventi, occorre rintracciare un evento in cui siano presenti due muoni (ricordiamo che i muoni proseguono pressoché indisturbati il loro percorso). Per esempio, si trova traccia di due muoni all’evento 6 del gruppo 1. Cliccando con il mouse sopra alla traccia relativa a uno dei due muoni, essa si illuminerà di rosa e utilizzando il tasto “Insert Muon”, la traccia entrerà a far parte di quelle di interesse: le sue caratteristiche saranno così riportate a destra della tabella contenente tutte le tracce. Occorre ora selezionare e inserire anche il secondo muone. Anche le sue caratteristiche compariranno a destra, creando così una nuova tabella. Se il primo muone è negativo, il secondo deve essere positivo, e viceversa.
La terzultima colonna della tabella, contrassegnata come mII [GeV], fornisce, date le caratteristiche dei muoni frutto del decadimento, la massa del bosone Z da cui essi hanno origine; in questo caso mZ = 90,54 GeV (1 GeV corrisponde a 1,78x10-27 kg).
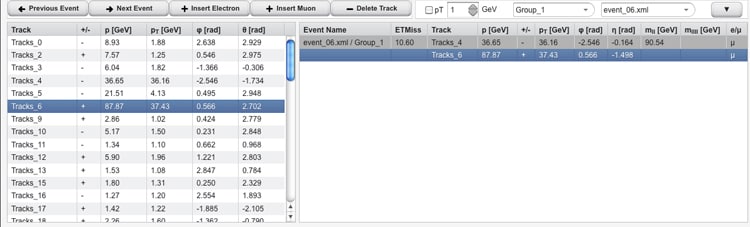
b. Occorre ripetere questa operazione analizzando tutti gli eventi del primo e del secondo gruppo. Per passare da un evento al successivo utilizza il tasto “Next Event”. In questo modo, è possibile riuscire a rintracciare 10 coppie di muoni, quindi 10 valori della massa del bosone Z. Per cambiare gruppo si utilizza il menù a tendina cliccando sulla freccia a lato della scritta Group_1.
c. Il programma fornisce automaticamente il valore di media e deviazione standard della popolazione. La scheda che segue, da utilizzare dopo aver svolto i passi precedentemente illustrati, può essere uno spunto per completare l’attività da svolgere in classe.
Soluzioni delle domande proposte
1. Masse ottenute in GeV: 90,54; 87,58; 87,88; 86,87; 90,27; 90,27; 83,93; 87,32; 94,94; 92,38; 97,66. mZ: (90 ± 7) GeV. Errore relativo: 8%
2. 0,003%. L’errore relativo ottenuto in questo esercizio è maggiore rispetto a quello ottenuto dai fisici perché la loro misura è stata ottenuta analizzando 4 500 000 decadimenti Z, contro le 10 misure di questo esercizio.
3. 1,6231·10-25 ± 0,0001·10-25 kg. L’errore relativo, se calcolato prima di approssimare, resta invariato, poiché valor medio ed errore assoluto sono moltiplicati per la stessa quantità.
4. È un istogramma: rappresenta quante volte si sono ottenuti i diversi valori di massa.