I frattali tra estetica e matematica

STORIE DI SCIENZA
Affascinanti oggetti matematici che ripresentano, a scale più piccole, la stessa struttura che hanno a scale più grandi: sono i frattali, scoperti dal matematico Mandelbrot e oggi utilizzati in moltissimi campi, dalla cosmologia alla medicina.
Centro di ricerca Thomas Watson dell’IBM, Stato di New York, 1979. Un matematico polacco educato in Francia, conclusa una dura giornata di lavoro, se ne va a casa. Sul tavolo lascia un foglio con sopra una macchia nera a forma di cuore con annesso un certo numero di regioni più piccole dai confini non troppo netti e, qui e lì, qualche puntino d’inchiostro.
È la rappresentazione grafica delle soluzioni di un problema al quale stava lavorando da anni. Benoit B. Mandelbrot, questo il nome del matematico, lascia un biglietto per il collega che lo precederà l’indomani mattina: «Occhio, queste macchie non sono dovute alla stampante, che funziona benissimo: c’è qualcosa da scoprire nell’insieme che stiamo studiando»
L’insieme di Mandelbrot
Nei giorni successivi, zoomando su quei punti d’inchiostro, Mandelbrot scopre che il contorno delle regioni nere ha una struttura di infinita complessità che riproduce in miniatura la medesima sequenza delle regioni più grandi. Ogni volta, cioè, che si ingrandisce l’immagine e si esplorano parti sempre più piccole, si trovano infinite repliche delle strutture macroscopiche dell’insieme. Nella figura di apertura potete vedere ingrandimenti successivi della macchia d’inchiostro stampata sul foglio quella sera del 1979: essa, nel suo complesso, viene detta insieme di Mandelbrot e la zona ingrandita in figura è chiamata Valle dei cavallucci marini.
Si tratta forse dell’esempio più famoso di oggetto frattale, una parola che Mandelbrot aveva già inventato per descrivere regioni composte di linee spezzate (dal latino fractus), dall’andamento apparentemente irregolare. Se fate un giro sul Web (per esempio su Wikipedia) potete esplorare in modo interattivo l’insieme di Mandelbrot a scale sempre più piccole e sperimentare, per usare le parole dello stesso studioso, un’esperienza di tipo estetico prima ancora che matematico.
Oggetti infinitamente simili a loro stessi
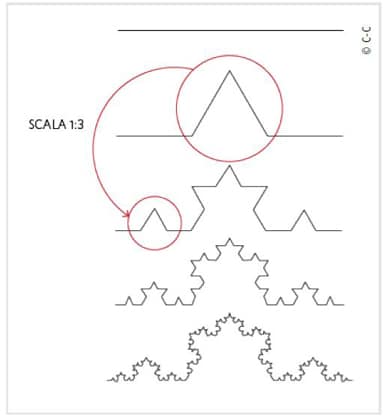
Il fascino dei frattali è legato soprattutto alla loro auto-similarità. Un insieme auto-simile è un insieme che ripresenta, a scale sempre più piccole, la stessa struttura che possiede a scale più grandi. Per chiarire questo concetto vi propongo un esempio famoso, quello del fiocco di neve. Con questo nome si indica una curva piana, inventata dal matematico svedese Helge von Koch nel 1904, che si può costruire seguendo la figura qui a fianco. Partite dal segmento della prima riga, dividetelo in tre parti uguali e rimuovete quella centrale; sostituite ora, al posto del pezzo rimosso, due lati di un triangolo equilatero. Avrete così una linea spezzata costituita da quattro segmenti (ciascuno dei quali lungo 1/3 del segmento originario) come quella della seconda riga. Ora passate alla terza riga ripetendo quanto appena fatto per ciascuno dei quattro segmenti della figura della seconda riga. La nuova linea sarà costituita da quattro tratti che sono copie in scala (1:3) della linea precedente. Potete immaginare di iterare questo procedimento tante volte. Ma tante quante?, potreste chiedervi. Bisogna che immaginiate di ripetere questa procedura all’infinito: ciò che otterrete “alla fine” è il fiocco di neve di Koch. Se provaste a guardare un pezzettino di questa curva con una lente d’ingrandimento, vedreste che su ogni lato ci sono triangoli equilateri e su ciascuno di questi ci sono triangoli equilateri più piccoli e via dicendo, in una struttura infinitamente frastagliata.
In effetti, la curva di Koch non è che un primo esempio di un insieme affascinante di oggetti auto-simili; nelle figure alla pagina seguente potete vedere immagini che richiamano altri due frattali famosi: la fiaschetta di Sierpinski e la spugna di Monger.

Come la vita nell’Universo
Se nel riflettere su oggetti di questo tipo avete provato un po’ di stupore, state pur certi di essere in buona compagnia. Il matematico napoletano Ernesto Cesàro, infatti, scrisse: «È questa similitudine tra il tutto e le sue parti, perfino quelle infinitesimali, che ci porta a considerare la curva di Koch alla stregua di una linea veramente meravigliosa tra tutte. Se fosse dotata di vita, non sarebbe possibile annientarla senza sopprimerla al primo colpo, poiché in caso contrario rinascerebbe incessantemente dalle profondità dei suoi triangoli, come la vita nell’universo». A proposito, per chi ha già studiato un po’ di analisi matematica, osserviamo che la curva di Koch è continua, ma è non derivabile in tutti i punti che la costituiscono.
Una nuova geometria
L’auto-similarità rappresenta un nuovo codice interpretativo nell’indagine della realtà: a differenza della geometria euclidea, così rigida nel rappresentare il mondo visibile, e talora così lontana dalle forme reali, la geometria dei frattali è capace di rappresentare i profili di una montagna o di una costa, le nuvole, le strutture cristalline e molecolari, e addirittura le galassie.
Nelle parole dello stesso Mandelbrot, «i frattali servono a trovare una nuova rappresentazione che parta dall’idea di base che il piccolo in natura non è nient’altro che una copia del grande».
La costa degli Usa
Per comprendere meglio l’intuizione di Mandelbrot e il successo della sua nuova geometria, consideriamo il famoso esempio della descrizione di una costa frastagliata. Se guardassimo su un atlante a larga scala la costa orientale degli Stati Uniti, essa apparirebbe come una linea liscia di circa 4000 km. Se considerassimo la stessa costa a una scala più fine, la vedremmo molto più frastagliata, e quindi anche più lunga.
Se fossimo a bordo di un aereo, potremmo valutare insenature e promontori e arriveremmo a dire che la sua lunghezza è di circa 8000 km. Se, invece, la percorressimo a piedi, dovremmo camminare per 25 000 km e se una formica longeva si mettesse nella stessa impresa, dovrebbe percorrere 50 000 km. Per descrivere in modo efficace la complessità di questa costa occorre pertanto una struttura auto-simile, la sola in grado di rendere conto di quanto succede a diverse scale di osservazione: usando una consueta curva della geometria euclidea, riusciremmo a rappresentare solo ciò che avviene a una certa scala (per esempio quella della veduta aerea), ma saremmo condannati a perdere tutte le informazioni sulla struttura più fine (per esempio quella osservata dalla formica). Infatti, le curve della geometria euclidea, quando si zoomano, si approssimano bene con delle rette, ma non accade così per i frattali: ogni volta che zoomiamo un frattale, da esso riemerge una curva altrettanto frastagliata di quella a scala superiore.
La dimensione di un frattale
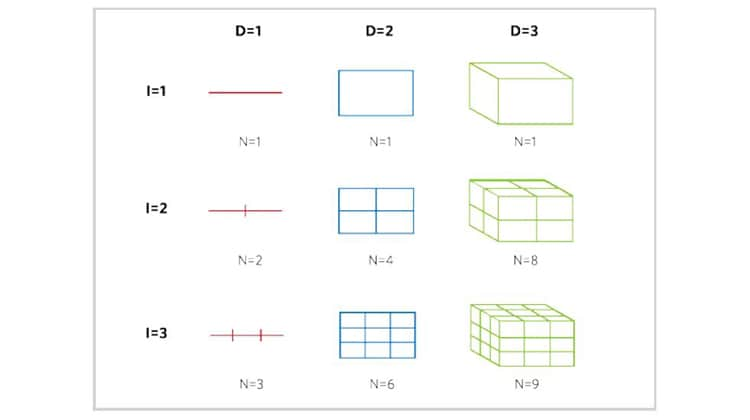
Le curve frattali del piano sono, per così dire, infinitamente frastagliate e riempiono il foglio in modo più “fitto” delle curve considerate dalla geometria euclidea. Mandelbrot insegnò a misurare queste proprietà dei frattali utilizzando un concetto di dimensione inventato dal matematico tedesco Felix Hausdorff nel 1918. Vediamo di che cosa si tratta. Nessuno ha esitazioni nel distinguere una figura bidimensionale da una tridimensionale: la nozione di dimensione classica (che si chiama dimensione topologica) ci risulta abbastanza familiare e intuitiva sin dall’infanzia (sebbene la definizione rigorosa sia in effetti un affare un po’ delicato). Curve come il fiocco di neve, però, hanno sollecitato i matematici a inventare un nuovo concetto di dimensione che è troppo tecnico per questo contesto, ma che può essere spiegato bene nell’esempio della curva di Koch e di altri oggetti auto-simili. Riflettiamo dapprima su una proprietà che distingue gli oggetti unidimensionali da quelli bidimensionali e tridimensionali in senso classico. Prendiamo, per esempio, un quadrato bidimensionale e immaginiamo di fare una fotocopia a scala del 50% (cioè un’omotetia di coefficiente ½): quanti quadrati rimpiccioliti servono per coprire il quadrato iniziale?
Ovviamente 4. E se riducessimo al 50% un cubo, quanti cubi occorrerebbero per riformare un cubo grande come quello iniziale? Questa volta sono 8. Ebbene, la dimensione di Hausdorff è quel numero n tale che (1/k)n = 4,8 ecc. , dove k è il fattore di scala. Nel caso considerato, quindi, k = ½ e quindi n = 2 per il quadrato e n = 3 per il cubo (osservate che, cambiando il coefficiente di omotetia, il risultato non cambia). Troviamo qui la conferma di una cosa che ci ha insegnato la maestra: il quadrato, che è una figura piana, ha dimensione due mentre il cubo ha dimensione tre. Passiamo ora alla curva di Koch e troveremo una sorpresa. Concentratevi sulla seconda riga della figura: se restringete la curva di un fattore 1/3 , avete bisogno di 4 pezzetti per riformare la curva (come descritta nella terza riga della figura). Quindi: (1: 1/3)n = 4 cioè 3n = 4, il che dà n = ln 4 : ln 3!
La cosa rilevante è che, questa volta, la dimensione di Hausdorff non è un intero, e, più precisamente, è un numero strettamente compreso tra 1 e 2. Alla scuola elementare ci hanno taciuto alcune cose importanti: esistono curve nel piano che sono così frastagliate da avere dimensione più grande di uno (e più piccola di due). Per quanto sconcertante, la possibilità di associare a oggetti geometrici una dimensione non intera, apre prospettive straordinarie che accenniamo brevemente di seguito. Va detto però che non tutti i frattali hanno dimensione non intera (per esempio l’insieme di Mandelbrot ha dimensione 2): potete apprezzare una bella classificazione di alcuni frattali in base alla loro dimensione al questo indirizzo.
A cosa servono i frattali?
Ai frattali associamo immagini suggestive come rilievi montuosi, cavolfiori, coste marine, fiocchi di neve, nubi, tutte caratterizzate da un’elegante simmetria interna e da un alto grado di “complessità microscopica”. In effetti l’applicazione di concetti e metodi propri della geometria frattale spazia in campi inaspettati: con modelli frattali si spiegano alcuni comportamenti dei mercati finanziari, in cosmologia si può descrivere la distribuzione della materia visibile luminosa, si può generare musica che assicura un buon equilibrio tra prevedibilità e sorpresa.
Non solo: la geometria frattale si usa per studiare gli organismi marini, i terremoti, la formazione dei fulmini. E di certo, quel giorno del 1979 il collega di Mandelbrot, davanti a un foglio pieno di macchie d’inchiostro, mai avrebbe immaginato che, in soli vent’anni, i frattali si sarebbero resi necessari per leggere una TAC o descrivere la struttura tridimensionale del genoma umano.
Che cos’è un’omotetia
Dato un punto O del piano e un numero reale k > 0, si dice omotetia (diretta) di centro O e rapporto k la trasformazione del piano che a O fa corrispondere O e ad ogni punto P≠O fa corrispondere un punto P’ tale che:
- P e P’ giacciano sulla stessa semiretta uscente da O;
- P’O : PO = k.
Si possono considerare anche omotetie inverse, in cui P e P’ giacciono sulla stessa retta passante per O ma da parti opposte. In questo caso si può convenire di parlare di rapporto negativo.