I modelli matematici

Strumenti impiegati per lo studio anche dei problemi sociali
MATEMATICA – II GRADO
Una diffusa spiegazione del concetto di modello matematico ci fa chiaramente capire che è uno strumento capace di darci una visione più ampia e ragionata di una problematica, anche quando si tratta di vita sociale. Come ci dimostra il periodo che stiamo vivendo, in cui l’interesse per i modelli matematici si è esteso ed è passato dalle aule scolastiche alle prime pagine dei giornali e ai talk show di prima serata, dove giornalisti e politologi si ritrovano a discutere di gaussiana e funzione esponenziale.
di Angelo Guerraggio
I difficili momenti che stiamo vivendo con il Covid-19 hanno portato all’attenzione dell’opinione pubblica il termine e la problematica dei modelli matematici. Il Paese ha scoperto quasi all’improvviso che, per fotografare e capire l’evoluzione di un fenomeno complesso quale un’epidemia, bisogna ricorrere (anche) alla matematica. Quello di modello non è certo un concetto nuovo per i ricercatori. Nella scuola, la “bandiera” dei modelli matematici è stata fatta propria dagli insegnanti che ritengono che la didattica più tradizionale sia poco astratta (magari lo fosse ed educasse al pensiero astratto!) ed esclusivamente concentrata sui calcoli e avulsa da qualsiasi riferimento alla realtà che possa intercettare l’attenzione dei ragazzi.
La novità venutasi a creare con l’attuale situazione sanitaria è che l’interesse per i modelli matematici si è esteso ed è passato dalle aule scolastiche alle prime pagine dei giornali e ai talk show di prima serata, in cui giornalisti e politologi si ritrovano a discutere di gaussiana e funzione esponenziale.
Che cos’è un modello matematico?
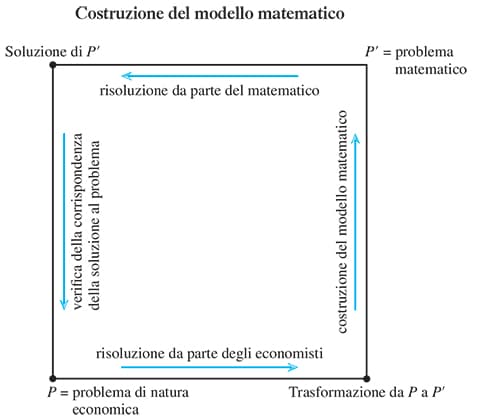
Lo raccontiamo attraverso un quadrato. All’inizio, ad esempio nel vertice in basso a sinistra del quadrato, c’è un problema P. Tutto ha inizio con un problema da risolvere; può essere tratto dalla vita quotidiana oppure consistere in una questione di fisica, di economia, di chimica, di matematica, ecc. Supponiamo che sia di natura economica. In una prima fase, gli economisti cercheranno di risolverlo tra loro con la logica ordinaria e gli strumenti della loro disciplina. In molti casi ce la faranno: molti problemi non hanno bisogno della matematica per essere risolti.
Il lato inferiore del quadrato, che stiamo percorrendo in senso antiorario, rappresenta (nel nostro esempio) proprio il lavoro compiuto dagli economisti per risolvere con il loro specifico linguaggio la questione. Così molti problemi, quelli che non hanno bisogno della matematica, escono dal quadrato e dal nostro racconto.
Rimangono quelli più difficili, quelli per cui gli economisti bussano alla porta del matematico in cerca d’aiuto. Ci stiamo dirigendo verso il vertice del quadrato in basso a destra. Il matematico capisce subito che la questione che gli viene sottoposta è troppo sfaccettata per essere trattata matematicamente: ci sono troppe variabili in ballo e sono troppe anche le relazioni che le legano. Si perderebbe molto tempo ad affrontare il problema com’e, oltretutto con un lavoro dall’esito incerto. Meglio semplificarlo, idealizzarlo, passando a un problema P’ che confermi nella sostanza il quadro offerto da P, ma in cui il numero delle variabili e delle relazioni sia minore, e in generale la situazione da analizzare sia meno complicata. Così il nostro matematico comincia a lavorare su P’.
Nel quadrato, il lato verticale destro rappresenta la vera e propria costruzione del modello. Si tratta ora di tradurre il problema P’ in un linguaggio matematico, ossia in formule. È una delle fasi più impegnative della modellizzazione di un problema perché non esistono regole prefissate per compiere l’operazione. È il momento in cui risalta maggiormente la creatività del matematico, già all’opera dal passaggio da P a P’ che può essere idealizzato in diversi modi e con la scelta di differenti aspetti rilevanti. Con buona pace di chi crede che la matematica sia una rigida e meccanica applicazione di regole, senza alcuno spazio per la fantasia, la costruzione di un modello dipende invece pesantemente dalla creatività del ricercatore, dalle sue scelte a proposito di ciò che in P è più significativo e della particolare sua trasposizione in un linguaggio matematico.
Siamo arrivati nel vertice del quadrato in alto a destra: P’ non è più un problema di carattere economico (nel nostro esempio), reale o ideale che fosse, ma è diventato un problema matematico. Si tratta ora di venirne a capo. A volte basta applicare una formula, altre volte la ricerca della formula o della teoria matematica che permetta di risolvere il problema può diventare complessa; addirittura può succedere che questa non esista ancora e debba essere inventata. La matematica è un linguaggio dinamico che si aggiorna continuamente per rispondere ai nuovi problemi che le vengono sottoposti.
Il lato superiore del quadrato appartiene per intero al piano matematico. La sua estensione esprime il lavoro dello studioso che cerca quel “pezzo” di matematica che gli serve, adatta teorie già elaborate o magari ne inventa di nuove e poi, finalmente, passa al calcolo. Quello che si impara a scuola (il calcolo, appunto) non è elemento estraneo alla complessa attività matematica descritta attraverso la costruzione di un modello, ma ne è una parte, che oggi non si fa più con carta e penna, ma si avvale di sofisticati programmi e veloci computer.
Siamo così arrivati nel vertice del quadrato in alto a sinistra: abbiamo trovato la soluzione del problema matematico in cui è stato tradotto P’. Non è finita però, il quadrato si deve chiudere; occorre verificare che la soluzione ottenuta sia corretta, non tanto nel senso della sua esattezza, quanto soprattutto della sua corrispondenza all’iniziale problema P. Si scende lungo il lato sinistro del quadrato per tornare sul piano della realtà e verificare empiricamente se il risultato trovato abbia risentito delle semplificazioni introdotte nel passaggio da P a P’. Se non risolve efficacemente il problema P, occorre ricominciare da capo e raffinare il modello adottando una semplificazione più contenuta o diversa.
Un modello matematico è dunque una rappresentazione idealizzata, nel linguaggio formale della matematica (le sue formule), di un “pezzo” di realtà. L’obiettivo è studiarlo, capirlo, prevederne l’evoluzione. Le conclusioni a cui giungeremo ci forniranno delle soluzioni approssimate perché dipendono dalla semplificazione che abbiamo dovuto operare del problema reale, quasi una sua caricatura, ma è un procedimento necessario per introdurre il linguaggio matematico che ci fa sperare di arrivare dove altri linguaggi non riescono a pervenire e di poter via via migliorare l’approssimazione raffinando il modello con dati iniziali sempre più precisi.
La grande novità dei modelli matematici è la consapevolezza che per capire la realtà (dicevamo che all’inizio del “quadrato” c’è sempre un problema) bisogna prenderne le distanze o, in altre parole, frapporre tra noi e il “pezzo” di realtà che vogliamo analizzare uno schermo, il nostro ragionamento. Non basta osservare; non basta fotografare la realtà; bisogna interpretarla con una caricatura che decida quali sono i tratti salienti, e magari li esasperi. Un modello matematico, in questo senso, è diverso dai “modellini“ in scala di una automobile o di una costruzione architettonica che si limitano, per così dire, a riprodurla fedelmente semplicemente rimpicciolendone le dimensioni in modo da poterla osservare con un unico sguardo.
Il passaggio dalla fotografia a una caricatura, dalla riproduzione fedele in scala dell’oggetto da studiare a una sua rielaborazione teorica, è un insegnamento che viene già da Galileo quando decide di trascurare i rumori di fondo, di “defalcare gli impedimenti della materia” e di concentrarsi sugli aspetti che valuta essenziali per il suo studio. I corpi non sono dei punti e l’attrito è ben presente sul piano inclinato, ma è proprio questa idealizzazione che permette di scrivere le prime pagine della meccanica.

Vito Volterra (3 maggio 1860 – 11 ottobre 1940)
Modelli matematici e pandemia
Dunque, è una strada lunga quella che porta ai modelli impiegati per fronteggiare l’attuale pandemia. Ripercorrerla, o anche solo accennarvi, ci dà l’opportunità di avere un’ulteriore conferma che le idee in matematica non nascono già perfette, ma vivono in un continuo lavoro di approfondimento e revisione.
Per noi, del percorso seguito dai modelli matematici, è particolarmente significativo il momento in cui non vengono più impiegati per lo studio dei soli problemi fisici, ma si aprono anche a quelli sociali. Non stiamo naturalmente parlando di un momento preciso ma del periodo, a cavallo tra Otto e Novecento, in cui i matematici capiscono che il loro linguaggio è talmente generale da poter essere impiegato in qualunque contesto, anche quello economico-sociale. È un clima ben rappresentato da Vito Volterra, il più importante matematico italiano del periodo. Invitato a tenere il discorso inaugurale dell’anno accademico 1901-2 all’Università di Roma dove insegnava, titola il suo intervento “Sui tentativi di applicazione delle matematiche alle scienze biologiche e sociali”. Avrebbe potuto trattare molte questioni interne alla matematica (era analista e fisico matematico) e sceglie invece di parlare delle nuove frontiere applicative.
Nella sua prolusione leggiamo una delle prime descrizioni di modello matematico:
“Plasmare dunque concetti in modo da poter introdurre la misura; misurare quindi; dedurre poi delle leggi; risalire da esse ad ipotesi; dedurre da queste, mercé l’analisi, una scienza di enti ideali sì, ma rigorosamente logica; confrontare poscia con la realtà; rigettare o trasformare, man mano che nascono contraddizioni fra i risultati del calcolo ed il mondo reale, le ipotesi fondamentali che han già servito; e giungere così a divinare fatti ed analogie nuove o dallo stato presente arrivare ad argomentare quale fu il passato e che cosa sarà l’avvenire; ecco, nei più brevi termini possibili, riassunto il nascere e l’evolversi di una scienza avente carattere matematico“.
La descrizione attraverso la metafora del quadrato delle caratteristiche salienti di un modello spiega come la matematica non si possa ridurre a calcolo, ma questo sia solo uno dei lati del quadrato, ovvero uno dei momenti dell’attività del matematico. Ci fa anche capire che l’astrazione non è una fuga da quello che anche Volterra chiamava “mondo reale”, ma una mossa talora indispensabile per guardarlo dall’alto, prenderne le distanze, vederlo in un’altra prospettiva. Davvero non ha senso stare a discutere se è “meglio” la matematica dell’utile o quella “teorica”; l’una è funzionale all’altra e sarebbe insensato rinunciare a una della due. È come se una persona, normalmente dotata di due gambe, decidesse di usarne solo una e fosse così costretto a saltellare su una gamba sola invece di camminare.
Referenze iconografiche: Jackie Niam / Shutterstock