Matematica come strumento di consapevolezza sociale: lezioni del, dal e col Covid

La competenza matematica è utile per la vita
MATEMATICA – SECONDO GRADO
Quando mai succede, nell’esperienza di docenti di matematica appassionati ma incompresi, che gli studenti stiano a sentire a bocca aperta, che chiedano insistentemente ulteriori delucidazioni? La matematica è troppo spesso percepita come arida e fredda. Purtroppo, l’epidemia di Covid è stata (ed è tuttora) un’ottima occasione per gli insegnanti di dimostrare agli studenti che la competenza matematica non è scollata dalle necessità della vita quotidiana, al contrario. La matematica può essere uno strumento certo di coscienza, ma forse anche di giustizia sociale.
di Silvia Benvenuti
L’Unione Europea individua, tra le otto competenze chiave di cittadinanza, quella matematica, definita come l’abilità di sviluppare e applicare il pensiero matematico per risolvere una serie di problemi in situazioni quotidiane. Effettivamente, l’attualità recente ci ha messo di fronte una realtà, quella della pandemia di Covid-19, in cui purtoppo di situazioni problematiche cui applicare la nostra competenza matematica ce ne sono di nuove ogni giorno.
Numeri, termini e grafici del terrore
10 marzo 2020: un’Italia confusa segue con apprensione la conferenza stampa del presidente del consiglio Giuseppe Conte. Dal giorno dopo, l’intera nazione è confinata: bar chiusi, ristoranti solo per l’asporto, proibiti gli spostamenti al di fuori della provincia di residenza, didattica a distanza per scuole e università, autocertificazioni subito obsolete che seguono il ritmo inquietante dei provvedimenti governativi.
Se facciamo un passo indietro a quei giorni, che oggi sono più che attuali ma sembrano lontani anni luce, ricorderemo senz’altro l’appuntamento fisso delle nostre giornate di reclusi: puntualmente, alle 18, il capo della protezione civile snocciola le cifre dell’epidemia, immediatamente riprese in tempo reale da tutti i quotidiani (vedi fig. 1). Cifre che, per la maggior parte della popolazione italiana, significano solo una cosa: terrore. Si parla di R0, di curva, di crescita esponenziale, di abbassare il picco, espressioni che per i più sono totalmente prive di senso ma che, nonostante questo, entrano presto a far parte del lessico comune della paura.

Fig. 1 Un esempio dei dati – Fonte: Sole 24 ore, versione on line
Ebbene: io credo che un qualunque matematico dotato di un minimo di senso civico si sia sentito, a seguito dell’ascolto di questi bollettini di guerra, chiamato in causa. Perché, se ci pensate bene, per fornire agli italiani sgomenti qualche chiave di lettura di questi numeri, termini e grafici così inquietanti, non è che servisse poi una matematica così avanzata. Con strumenti tutto sommato di base era già possibile diradare molto la nebbia dell’ignoranza, consentendo di chiarire il senso di dati altrimenti difficili da interpretare.
La matematica è capace di spiegarci perché, se vogliamo abbassare questo benedetto “picco”, sia necessario stare in casa, lavarsi le mani e mettersi le mascherine; la matematica è capace di spiegarci perché, se ieri c’erano 3000 nuovi contagi, non è affatto strano che oggi ce ne siano 8000 e domani 30.000, se non facciamo nulla per contrastare la diffusione di un virus con sviluppo esponenziale. La matematica rende le notizie (più) trasparenti e le persone (più) consapevoli, e come tali (più) inclini ad aderire a indicazioni che, altrimenti, potrebbero suonare come imposizioni di cui non si comprende la necessità e cui ci si assoggetta, se va bene, obtorto collo. La matematica ci aiuta a non cadere dal pero. La matematica, e scusate se è poco, ci allontana dalla follia negazionista. La matematica, in un momento come quello attuale, può essere uno strumento certo di coscienza, ma forse anche di giustizia sociale.
Matematica contro la paura: Covid e justification problem
Tra marzo e aprile 2020 io l’ho fatto, questo esperimento: ai miei studenti matematici, ai miei futuri maestri, agli amici, agli insegnanti che ho incontrato in corsi virtuali di formazione, a mio figlio e ai suoi compagni ho cercato di dare un kit minimale di nozioni matematiche atte a tradurre le informazioni dei telegiornali per farle proprie. Se state pensando “poverini, che pizza”, per una volta siete sulla cattiva strada: perché nulla stimola l’attenzione e la voglia di imparare quanto la motivazione forte data dall’urgenza, dal bisogno di capire, che una situazione di emergenza come questa necessariamente portava con sé. Se mi perdonate il cinismo, l’epidemia di Covid-19 è stata (ed è tuttora) un’ottima occasione per gli insegnanti di matematica.
Pensateci: quando mai vi succede, nella vostra esperienza di docenti di matematica appassionati ma incompresi, che i vostri studenti vi stiano a sentire a bocca aperta, che chiedano insistentemente ulteriori delucidazioni, che vogliano riportare in famiglia quello che hanno ascoltato in classe (reale o virtuale)? La nostra materia purtroppo è troppo spesso percepita come arida e fredda, del tutto scollata dalle necessità della vita quotidiana. La si vede come un blocco monumentale di formule e calcoli del tutto privi di senso e, soprattutto, del tutto inutili. Di conseguenza, il primo (in termini sia di tempo che di importanza) compito di un buon insegnante di matematica è far capire ai suoi studenti che la competenza matematica è utile per la vita, non per l’interrogazione.
Ebbene la Covid-19 – che tanto ci ha tolto e ci sta togliendo in termini di libertà personali, serenità e, purtroppo, vite umane – ha fornito agli insegnanti di matematica di tutti gli ordini e gradi un campionario virtualmente inesauribile di problemi di realtà che, essendo tanto vicini all’esperienza quotidiana dei nostri studenti, sono di sicuro successo nel suscitare la loro attenzione. Questo naturalmente non consola, ma tanto vale approfittarne.
Per tutti: cosa si intende con crescita esponenziale
Uno dei termini che più ricorrono in questi giorni di pandemia, “esponenziale”, è davvero semplice da spiegare a studenti di ogni età, a partire da quelli della scuola primaria. Lo si può descrivere, infatti, facendo in primo luogo ricorso a una leggenda, quella dell’invenzione del gioco degli scacchi.
Il re della Persia chiamò un famoso mago, Sissa Nassir, e gli disse: “Inventa per me un gioco bellissimo, che io lo possa giocare in ogni momento, e che sia imperituro”. Sissa inventò gli scacchi e li donò al re che tanto fu contento che gli disse: “Hai superato te stesso; chiedimi come ricompensa quel che vuoi e sarai accontentato”. E Sissa chiese, semplicemente, un po’ di riso. “Come un po’ di riso”, ribatté il re incredulo e divertito. “Chiedi di più, quel che vuoi”. Ma Sissa insisté, finché il re disse: “E sia, tutto il riso che vuoi ti sarà dato”. E chiamò il gran ciambellano, che era anche l’abacista di corte. Sissa chiese un granello di riso per la prima casella, due per la seconda, quattro per la terza, e così via sempre raddoppiando, fino a completare le caselle della scacchiera che lui stesso aveva inventato. Il re rise a crepapelle, pensando: “Che idiota, poteva avere metà del mio regno!”. Ma il gran ciambellano sbiancò in volto. Si rivolse al re e disse: “Maestà, temo che non potremo accontentare Sissa Nassir”. “Oh, e perché?” chiese il re allibito.
Chiedetelo ai vostri alunni: quanti granelli di riso si ottengono, a partire da uno solo, se a ogni casella della scacchiera raddoppiamo il numero dei chicchi? Guardatelo insieme in questa animazione: sarà subito evidente che si tratta di una quantità enorme.
Se consideriamo che 10 chicchi pesano circa 10 grammi possiamo dire che il Re di Persia avrebbe dovuto consegnare a Sissa 1.800.000 milioni di tonnellate di riso, ovvero la produzione mondiale di riso di ben tremila anni!
E il ciambellano fece presente al re che anche raccogliendo tutto il riso di Persia e di Cina e di India e di ogni terra emersa, non solo il riso del raccolto attuale, ma il passato e il futuro nei tempi dei tempi, mai e poi mai si sarebbe ottenuto tanto riso, il cui valore superava di miliardi di volte quello del reame stesso. E così finì che Sissa Nassir fu decapitato per alto tradimento reale e il ciambellano fu condannato a fare i conti di quanto riso era quello richiesto…
Se con i ragazzini più giovani ci fermeremo qui, a mano a mano che crescono le loro competenze matematiche potremo approfondire il conto: quello dei grani di riso di Sissa, per esempio, consiste nel calcolare
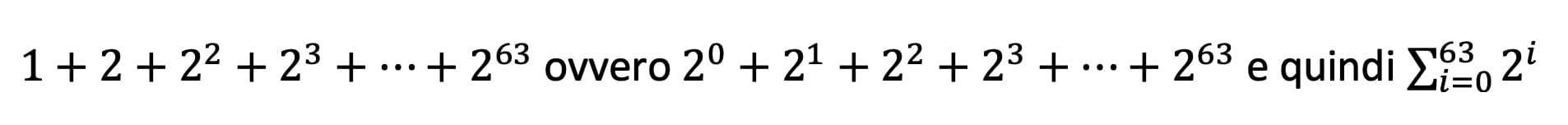
Si tratta quindi della somma parziale di 64 termini di una progressione geometrica di ragione 2, il cui risultato si calcola facilmente grazie alla comoda formula corrispondente.
Ma cos’hanno in comune scacchi e Covid-19?
Ebbene: la crescita dei contagi di un’epidemia funziona proprio come quella dei chicchi di riso sulla scacchiera, ovvero in modo esponenziale. Spieghiamolo meglio: immaginiamo di avere a che fare con una malattia caratterizzata dal fatto che ogni individuo infetto contagi, in media, altri due individui. Al primo passo, abbiamo un solo infetto, che infetterà due suoi contatti; a loro volta, questi infetteranno due contatti ciascuno, e così via: la malattia, in altri termini, si propagherà raddoppiando a ogni passo il numero di nuovi contagiati... ovvero il numero di nuovi contagi cresce esattamente come i grani di riso sulla scacchiera di Sissa! Qui trovate un bel video che lo spiega.
Un passo avanti: picco, R0, stupidario Covid
Fatta questa semplice introduzione, siamo in grado di presentare agli studenti che hanno un minimo di familiarità con i grafici di funzione un altro protagonista indiscusso dei dibattiti televisivi degli ultimi mesi, il famigerato R0. Si tratta del rapporto riproduttivo di base ovvero di quel numero, diverso per ogni malattia, che indica il numero di individui che vengono contagiati, in media, da ogni individuo infetto. Al suo esordio sulla scena internazionale, il Covid-19 aveva un R0 pari a circa 2,5, surclassato da altre malattie più o meno comuni quali il morbillo (16-18), la parotite (10), il vaiolo (3-5), l’Hiv (2-5), la malaria (addirittura > 100). In una malattia con rapporto riproduttivo R0, il numero di nuovi positivi cresce come (R0)x, ovvero come possiamo vedere nella Figura 2.
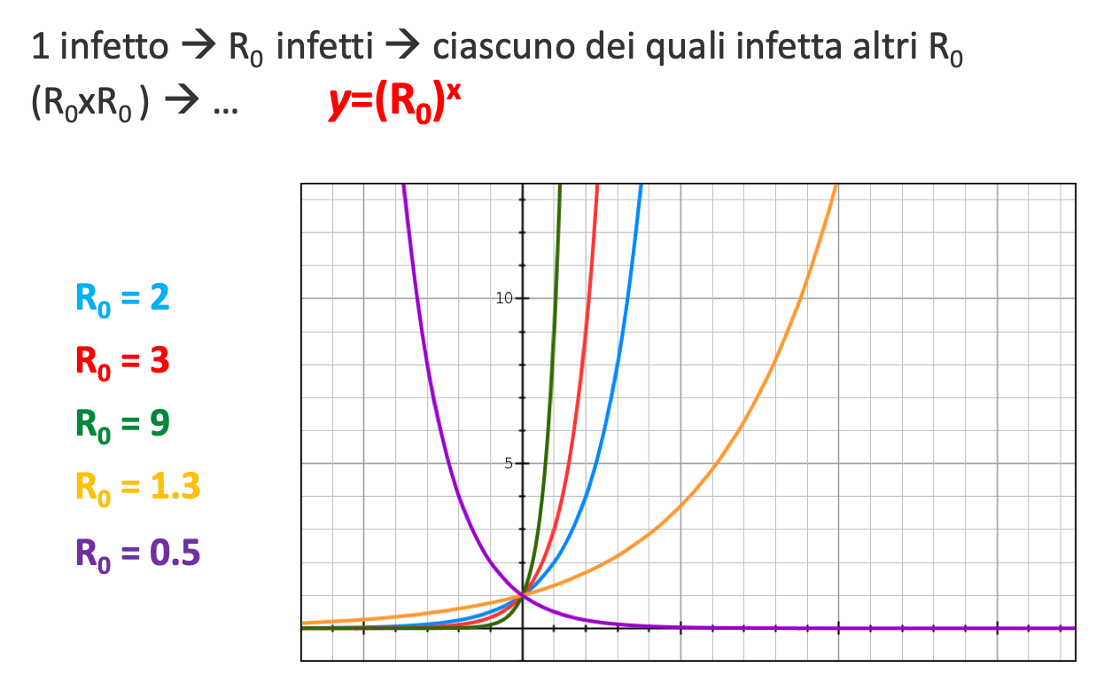
Fig. 2 Se R0 cresce, la curva corrispondente è più ripida: R0 misura quindi la rapidità con cui la malattia si diffonde. Se R0 <1, la curva invece decresce, ovvero la malattia va a esaurirsi – Immagine di Silvia Benvenuti.
Ora: abbiamo affermato che ai suoi esordi la Covid-19 aveva R0 pari circa a 2,5 (ma per semplicità di calcolo arrotondiamo a 2). Tuttavia, questo numero di riproduzione è sensibile ai comportamenti umani: se, paradossalmente, riuscissimo a isolare completamente tutti gli infetti, da quel momento in poi bloccheremmo tutti i contagi, azzerando di colpo l’epidemia. Questo di fatto è praticamente impossibile, ma tutto sommato non è neppure necessario: supponiamo infatti di isolare a ogni passo 1/3 degli infetti; come spiegato nella sequenza di Fig. 3 (sinistra), questa misura sarebbe sufficiente a ridurre l’R0 a 1,3, mentre isolare a ogni passo i 2/3 degli infetti come in Fig. 3 (destra) ci porterebbe a un l’R0 di 0,6 che, automaticamente, costringerebbe l’epidemia a esaurirsi. Guardatelo qui.

Fig. 3 Effetti del confinamento sull’R0: confinamento più blando (sinistra), confinamento più deciso (destra) – Immagini di Silvia Benvenuti.
Questa semplice osservazione da un lato dovrebbe far capire il perché di misure impopolari come il tanto discusso lockdown, e dall’altro dovrebbe stimolare nei ragazzi un’osservazione banale ma matematicamente significativa: se il tasso di riproduzione è una grandezza variabile, chiamiamola piuttosto Rt (come in effetti finalmente si inizia a vedere sui giornali)! Sempre a partire da questa osservazione potrebbe farsi strada la spiegazione di cosa sia il famoso “picco”: ammettiamo (ipotesi purtroppo drammaticamente poco lecita nella circostanza specifica del Covid-19) che, una volta guarito (o deceduto), un individuo prima infetto non possa tornare a infettarsi; chiamiamo “rimossi” gli individui così usciti di scena; allora il numero dei nuovi contagiati non può continuare ad aumentare indefinitamente (non fosse altro che perché a un certo punto si esauriscono i possibili contagiandi); sicuramente, anzi, il numero dei suscettibili è sempre decrescente e il numero dei rimossi è sempre crescente (a meno che i tempi non siano tanto lunghi da dover considerare anche le nascite); finché vi saranno più contagi che rimozioni l'epidemia resterà nella sua fase ascendente, ma quando cominceranno a prevalere le rimozioni si entrerà nella fase discendente. Il momento del passaggio di andamento è il cosiddetto “picco”.
Gli articoli comparsi sui giornali negli ultimi mesi consentono inoltre di portare avanti una riflessione davvero utile su quale sia la cultura matematica espressa dalla nostra classe dirigente. Senza voler prendere in giro nessuno, ma anzi nella drammatica consapevolezza dell’ignoranza diffusa, credo che un’occhiata allo stupidario Covid possa essere significativa, per i nostri studenti (e per noi stessi). Le regole per la riapertura dei ristoranti nella fase 2, per esempio, hanno dato luogo a interpretazioni grafiche e commenti davvero tragicomici, ripresi da tutti i social, e non vi sarà difficile trovarne traccia. Sicuramente sarà interessante analizzarli in classe.
Conclusioni
L’analisi dello stupidario Covid evidenzia come, più che competenza matematica, gran parte della popolazione adulta del nostro paese (ma gli altri non stanno meglio) sembri esprimere piuttosto una forma grave di analfabetismo numerico. Grave sia perché concerne l’ignoranza di strumenti matematici davvero di base, sia soprattutto perché, in un momento di emergenza come questo, essere incapaci di decifrare le informazioni matematiche che ci arrivano dai media può essere davvero pericoloso. Se arrivare agli adulti non è facile, come insegnanti abbiamo però la possibilità di agire sui loro figli, contribuendo a creare cittadini che, forse, saranno adulti più consapevoli e come tali più responsabili. Non sprechiamo l’occasione.