Mateturisti in gita…virtuale!

Due itinerari virtuali alla scoperta delle bellezze matematiche
MATEMATICA
Le gite fuori porta per gli insegnanti di matematica sono occasioni in cui l’apprendimento della propria materia non è al primo posto. In questo periodo in cui non sono possibili gli spostamenti, invece, domandando la complicità dei colleghi di lettere e storia dell’arte, nulla vieta di mettere in piedi un’interdisciplinare gita virtuale che tenga in conto, oltre dell'aspetto storico e artistico delle bellezze da visitare, anche la matematica che ne ha reso possibile la realizzazione.
di Silvia Benvenuti
Diciamocelo: per noi insegnanti di matematica, la gita scolastica non è mai stata un momento professionalmente edificante. Tradizionalmente, il nostro ruolo si riduce a tenerli in fila abbaiando come cani da pastore, assicurarci di non lasciare a terra nessuno, supplicarli che non distruggano l'albergo, controllare che non si stonino (troppo) con alcol, fumo o altro che non possiamo nemmeno immaginare, convincerli che se vogliono a tutti i costi passare la notte in una stanza che non è la loro, è comunque preferibile che facciano il trasferimento via corridoio anziché sospesi tra finestra e finestra a 5 piani di altezza, e tutte le varie incombenze di carattere sbirresco a cui la nostra disciplina ci ha relegato da sempre.
Ebbene, è arrivato il momento della riscossa: in primo luogo, perché l’unica gita che possiamo fare in questo momento, grazie al Covid, è quella virtuale, per cui il cane da pastore automaticamente diventa superfluo. In secondo luogo perché, magari contando sulla complicità dei colleghi di lettere e storia dell’arte, nulla vieta di mettere in piedi un’interdisciplinare gita virtuale che sia, invece che meramente turistica, mateturistica. In altri termini ci proponiamo di tenere in conto, oltre all'aspetto storico e artistico delle bellezze che andremo a visitare, anche la matematica che ne ha reso possibile la realizzazione. E questo non tanto perché è servita come strumento tecnico – che gli edifici senza un paio di conti non stanno su lo sanno tutti, figuriamoci una pisana come me – ma soprattutto perché è servita come strumento creativo, suggerendo all'artista, all'architetto, al designer e in generale all'autore dell'opera soluzioni nuove e inattese.
Capisco che detto cosi possa lasciare un po' perplessi. Per convincervi, passo a illustrarvi un paio di esempi, pescando tra le destinazioni “classiche” per lo studente italiano, che naturalmente in questa veste di classico non avranno nulla: parafrasando Proust, il nostro sarà un vero viaggio di scoperta, non perché visiteremo nuove terre, ma perché lo faremo con nuovi occhi…e inusuali strumenti virtuali!

Gita del primo anno: antiche fortificazioni “alla moderna”
Qui prendiamo in esame un esempio specifico, quello di Lucca, ma fortificazioni analoghe – e analoghi tour virtuali – si trovano per tutta Italia, quindi non vi sarà difficile adattare quello che diremo alla vostra cinta muraria preferita. Per quanto riguarda quella di Lucca, va detto che si tratta di un esempio particolarmente interessante, visto l’ottimo stato di conservazione. Lo strumento virtuale che potete usare è questo Tour Virtuale – THINKlab, o uno qualunque degli innumerevoli tour delle mura che i vostri studenti saranno molto più abili di voi a reperire. Lasciate che vi consiglino loro, in modo da incontrarvi su un terreno comune: lasciando che mostrino le loro competenze da nativi digitali, avrete miglior fortuna quando spiegherete loro cosa vale la pena di guardare nei 103.209.450.000 video che vi proporranno.
Le mura di Lucca sono un esempio paradigmatico di fortificazione “alla moderna”, termine che individua la tecnica con la quale, in Europa, le fortificazioni realizzate nel corso del Medioevo vennero modificate, a partire dal Quattrocento, per rispondere a esigenze difensive profondamente mutate.
Scrive in proposito Niccolò Tartaglia, nel suo libro Quesiti et inventioni diverse pubblicato da Venturino Ruffinelli nel 1546: «Io dico che fortificare una città vi occorre la materia e la forma, che lo ingegno dell’huomo se approva per la forma delle sue mura, e non per la grossezza di quelle». Ovvero: se vogliamo proteggere adeguatamente una città, dobbiamo farlo scegliendo con intelligenza il materiale da costruzione e la forma delle sue mura, perché farle spesse non è sufficiente. Questa attenzione da parte di un importante matematico non deve stupirvi: è infatti proprio ai matematici che si deve lo sviluppo dell’architettura militare del periodo, in quanto tutti i problemi soggiacenti sono di natura eminentemente geometrica. Le cinte medioevali progettate a partire dal XII secolo, infatti, erano costituite da tratti di mura ad andamento rettilineo, dette cortine, generalmente (quasi) perpendicolari al suolo, intervallate da numerose torri. Sulla sommità delle mura si tracciava un cammino di ronda, da cui controllare la situazione, e un parapetto sormontato da merli. L’efficacia di una fortificazione era quindi legata soprattutto alla sua altezza: più una muraglia era alta, più lontano avrebbe consentito di guardare e più difficile sarebbe stato scalarla.
Per difendersi, inoltre, si faceva uso della cosiddetta “difesa piombante”, consistente nel getto dall’alto di pietre, olio bollente e pece fusa, a cui si aggiungeva l’offensiva degli arcieri appostati attraverso le feritoie o fra le merlature. La situazione mutò radicalmente con lo sviluppo delle artiglierie portatili: nel momento in cui i progressi della metallurgia permisero di costruire cannoni sempre più potenti, aumentandone progressivamente la gittata, non era più necessario, per abbattere una muraglia, farsi sotto con gli arieti, ma si poteva prenderla a cannonate da centinaia di metri di distanza. In questo senso, più una fortificazione era alta più costituiva un bersaglio facile: quello che nelle epoche precedenti era un punto di forza, si traduceva irrimediabilmente in un tallone d’Achille. Era necessaria, a quel punto, una riforma radicale della strategia difensiva, che chiamava in causa a gran voce “lo ingegno dell’huomo” evocato da Tartaglia.
Nel vostro giro virtuale, assicuratevi di dare adeguata rilevanza all’idea che sta al cuore della fortificazione “alla moderna” ovvero quella di baluardo (o bastione). Il teorico di riferimento è in questo caso Francesco Di Giorgio Martini, autore tra il 1481 e il 1484 del codice Ashburnham 361 conservato alla Biblioteca Medicea Laurenziana di Firenze, trattato in cui per la prima volta compare questo elemento architettonico: l’idea è che le torri andavano sostituite con strutture più basse, più massicce, generalmente a pianta pentagonale (ovvero a “punta di lancia”), cui venne dato appunto il nome di bastioni o baluardi. A seconda della conformazione dei luoghi, i baluardi assumono in realtà una grande diversità di misure e di angoli, ma sempre come varianti dello stesso modulo-base.
Le mura di Lucca ne presentano ben undici, di cui cinque di mateturistico interesse: baluardi San Colombano, La Libertà, San Martino, San Frediano, Santa Croce.
La storia delle mura, naturalmente, può portarvi molto più lontano: qui vi lasciamo con questo bel video Mura di Lucca - la storia | Turismo Lucca, rimandandovi ai consigli bibliografici per ulteriori approfondimenti.

Gita di quinta: Barcelona!
La prassi delle gite di quinta è quella di visitare destinazioni estere, sancendo in questo modo la (quasi) raggiunta maturità dei nostri studenti. Visto che Barcellona è una delle destinazioni più amate dagli italiani, concentriamoci su di lei, e sul tour virtuale degli edifici progettati da uno dei suoi architetti più iconici, Antoni Gaudí – quello della Sagrada Família, per intenderci. Ne trovate a bizzeffe, scegliete il vosto preferito online.
In questo caso, la prima cosa che dovrete far osservare ai ragazzi è l’ubiquità, nell’opera del catalano, delle superfici curve, nella convinzione che «La linea retta è la linea degli uomini, quella curva è la linea di Dio»: in quanto fervente cattolico, infatti, Gaudí voleva costruire a onore di Dio, e quindi imitando la natura, sua meravigliosa creazione, chiaramente caratterizzata da superfici curve e irregolari. È per questo che nei suoi palazzi non c’è un muro a piombo né una linea diritta, ma tutto è curvo. Tuttavia, costruire in pietra superfici curve è un’operazione nient’affatto banale, che Gaudí, che fortunatamente un po’ di matematica se l’era studiata, risolse scegliendo la giusta famiglia di superfici da costruire, quelle che chiamiamo superfici rigate.
Si tratta, per definizione, di quelle superfici che si ottengono facendo scorrere una linea retta su un profilo predeterminato: se per esempio si fa scorrere una linea retta verticale parallelamente a sé stessa lungo il profilo di una linea retta orizzontale, si ottiene il piano, che per definizione è quindi una superficie rigata; se invece la retta verticale si fa scorrere lungo il profilo di una circonferenza posta su un piano perpendicolare, si ottiene il cilindro, anch’esso quindi superficie rigata.
Questi due esempi non interessano Gaudí, essendo il primo assolutamente non curvo, e il secondo assolutamente non originale: gli vengono in aiuto altre rigate più creative, dai nomi esotici quali iperboloide a una falda, paraboloide iperbolico, elicoide e conoide.
La vostra ricognizione, virtuale o meno, dell’opera dell’architetto catalano, non può dirsi completa se non scoprite qualcosa del suo modus operandi: Gaudí, in modo abbastanza sistematico, progettava i suoi edifici utilizzando strani oggetti detti modelli stereo-funicolari. Appesa una bella tavola di legno al soffitto, si muniva di catenelle di varie lunghezze, ne fissava alcune per gli estremi alla tavola e altre alle prime in punti opportuni, lasciando poi che si disponessero tutte naturalmente sotto l’effetto della forza di gravità, a costruire quello che a prima vista si sarebbe detto un lampadario barocco. A questo punto, non restava che mettere uno specchio sul pavimento: il lampadario riflesso rivelava la sua vera natura, quella di scheletro di un edificio complicatissimo, avente come ingredienti fondamentali l’arco catenario e un suo parente, l’arco funicolare, che dà il nome al modello stesso.
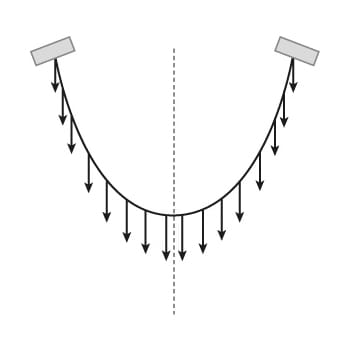
Si chiama catenaria la curva descritta da una catenella o da una corda tenuta per gli estremi e lasciata pendere, soggetta soltanto al proprio peso. La sua forma assomiglia alla più comune parabola, ma ha un’equazione più complessa, che chiama in causa il coseno iperbolico invece che un semplice polinomio di secondo grado.
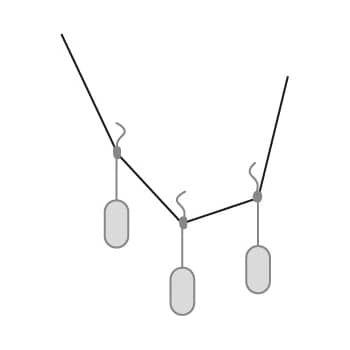
Se poi alla fune di cui sopra, fissata per i due estremi, si appendono diversi carichi puntuali (cosa che Gaudí faceva appendendo alle sue catenelle sacchetti pieni di pallini di piombo, o attaccando in un punto intermedio di una catenella l’estremo di un’altra), si ottiene una nuova curva, detta funicolare, che non è altro che una catenaria a tratti.
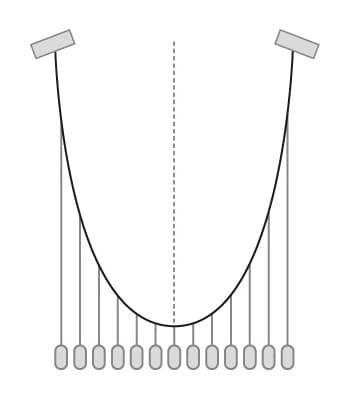
In particolare, se i carichi appesi sono orizzontalmente uniformi, la funicolare ottenuta è proprio una parabola.
Le curve ottenute in questo modo sono soggette solamente a forze di tensione, quindi se le ribaltiamo, ovvero facciamo l’operazione di riflessione che Gaudí otteneva con lo specchio, otteniamo archi, detti rispettivamente catenari e funicolari, soggetti esclusivamente a forze di compressione. Di conseguenza, grazie alla sua forma, lungo un arco catenario il carico è distribuito in modo omogeneo e per questo, a differenza di altri tipi di arco quale quello romano (a tutto sesto) o quello gotico (a sesto acuto), l’arco catenario sta in piedi senza bisogno di contrafforti o altri elementi di supporto. Inoltre è una struttura ottima nel senso (tecnico) che, a parità di materiale di costruzione, è quella di minimo peso in grado di sopportare un carico fissato. È l’arco perfetto, insomma, che con Gaudí, e quindi all’inizio del Novecento, fa il suo debutto in architettura.
Certo, lasciare (anche solo virtualmente) la capitale catalana senza fare un saltino a Figueras, dove si trova la casa museo di un altro dei suoi artisti più iconici, Salvador Dalí, è proprio un peccato: ma abbiamo esaurito le battute a nostra disposizione, quindi non possiamo far altro che rimandarvi ai riferimenti bibliografici consigliati.
Referenze iconografiche: Lucas Thai / Shutterstock, Incredible KB / Shutterstock, D-VISIONS / Shutterstock
Per approfondire
Aa.Vv, Matemilano. Percorsi matematici in città, Springer, 2004.
Aa.Vv, Con altri occhi. Sguardi matematici e non sulla città, Electa, 2005.
S. Benvenuti, Insalate di matematica 3. Sette variazioni su arte, design e architettura, Sironi, 2010.
S. Benvenuti, Matematica per creativi, XLaTangente n.24/2011, p. 20-23,
S. Benvenuti, Mateturisti a Milano, Linx Magazine n.15/2013, p. 40-47
S. Benvenuti, Il dinamismo plastico di Boccioni. In: AA.VV.. Rivista Mate. Matematica da zero a infinito, numero VIII. p. 64-67, 2016
S. Benvenuti, La sregolatezza regolata di Salvador Dalí. In: AA. VV.. Rivista Mate. Matematica da zero a infinito, vol VI. p. 66-69, 2016.
S. Benvenuti, Catastroficamente creativo: Salvador Dalí e la matematica. In: AA.VV.. (a cura di): Claudio Mazzanti, Dalí Experience.. p. 56-65, 2017.
S. Benvenuti, Congetture isomorfe, 2017.
S. Benvenuti, Genio e regolatezza: le passioni matematiche di Salvador Dalí, 2017.
S. Benvenuti, GM. Todesco, L. Cenci. Catastroficamente creativo: Dalí e la quarta dimensione, 2017.
S. Benvenuti, La faccia matematica del poliedrico Leonardo Da Vinci, Prisma magazine, marzo 2019.
S. Benvenuti, Piero della Francesca: poliedri e prospettiva alla corte dei Montefeltro, Prisma magazine, ottobre 2019.
S. Benvenuti, Toscana matematica, edizioni MathUp, in uscita con Prisma, Giugno 2021.
S. Benvenuti, In viaggio con i numeri: 12 itinerari per mateturisti curiosi, Edt, Giugno 2021.
S. Duvernois, G. Mele, M. Rossi (ed). Milano - maths in the city - a mathematical tour of Milanese architecture, 2012.
S. Lucente, Itinerari matematici in Puglia, Giazira, 2016.
S. Lucente, Itinerari matematici in Basilicata, Giazira, 2019.
D. Luminati, Matetrentino, percorsi matematici a Trento e dintorni, Springer, 2006.

Il nuovo marchio per l’area scientifica della Scuola secondaria di I e II grado: una proposta integrata di prodotti e servizi per rispondere al sempre più decisivo ruolo delle discipline scientifiche nella formazione degli studenti.