Matematica e Design

La vita quotidiana nasconde tantissime applicazioni della matematica
MATEMATICA
Insegnare la matematica attraverso le sue applicazioni nella vita quotidiana rende la materia più interessante per gli studenti. Prendendo in esame un'applicazione pratica di quadrilatero articolato, approfondiamo nell'articolo la relazione tra matematica e design.
di Silvia Benvenuti
L’anello di fidanzamento
Ebbene sì, sono stata sposata, tutto sommato con una certa soddisfazione, maturando perfino buoni ricordi e per un tempo incredibilmente lungo, conoscendomi. Che c’è di male, penserà l’incauto lettore. Be’, ecco, non ho chiarito un dettaglio cruciale: il marito in questione era ingegnere. Come se non bastasse, nella tassonomia già di per sé peculiare della famiglia Ingegneribus familiaris, il soggetto in esame apparteneva a una varietà particolarmente pericolosa: aerospatialis. Nonostante ciò, quando lo conobbi mi parve innocuo.

Che l’operazione non fosse del tutto immune da rischi avrei invece dovuto capirlo subito, quando il suddetto, in veste di aspirante fidanzato, si presentò, invece che col classico solitario («Che banalità!», fu il suo commento), brandendo un’inquietante fede turca a 54 fili. La peculiarità di un anello simile è il fatto che, sebbene possa essere infilato con facilità, una volta tolto dal dito è estremamente difficile da rinfilare nel modo corretto, ricostruendo l’esatto intreccio dei suoi fili.
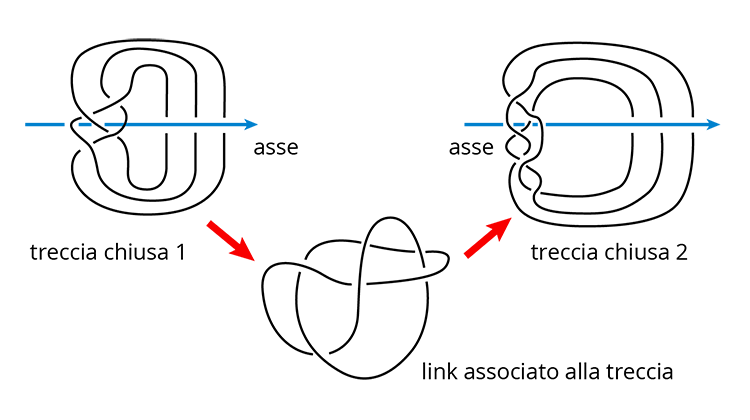
Questo perché sebbene i suoi componenti, essendo di metallo, siano rigidi – e quindi oggetti geometrici, il che fornisce un qualche aiuto – dal punto di vista topologico, una volta infilato, è la realizzazione di un oggetto astratto detto treccia chiusa. Nel momento in cui si sfila la fede dal dito, la treccia si trasforma in un link – termine tecnico traducibile con grande verosimiglianza in garbuglio – ovvero un oggetto matematico composto da più anelli, eventualmente annodati, allacciati tra loro.
A questo punto, rinfilarla nel modo corretto è un’impresa: infatti, mentre a ogni treccia corrisponde un unico link, il viceversa non è vero, cioè a uno stesso link possono corrispondere più trecce chiuse. In termini tecnici, si dice che uno stesso link può essere pettinato in modi diversi. Non vi dico gli esamini a cui mi sottoponeva: una volta avevo sbagliato la posizione del dito, quella dopo avevo sbagliato la pettinatura… ce n’era sempre una.
La fede nuziale
Come fede nuziale si limitò fortunatamente a propormi un banale nastro di Moebius. Per farvi un’idea di che forma abbia, prendete una striscia di carta, lunga e sottile, con le facce di colori diversi: incollando tra loro i lati corti otteniamo un cilindro; se invece li incolliamo dopo aver fatto una mezza torsione, otteniamo appunto il nastro di Moebius.

La bicolorazione, che permane nel cilindro, svanisce nel nastro di Moebius, dove la faccia di un colore viene saldata con quella dell’altro: rappresentando la fusione di due facce in una, questa figura si presta quindi assai bene a simboleggiare la fedeltà e il vincolo più o meno sacro del matrimonio. Peraltro, visto l’esito del mio, non so se mi sentirei di consigliarvela…
Il letto contenitore
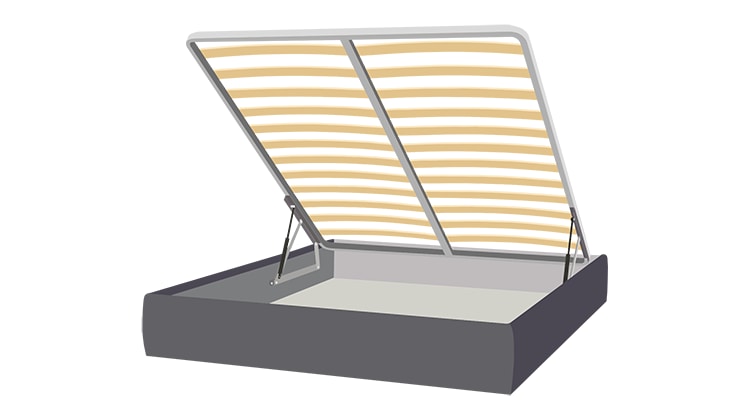
Ad ogni modo il vero problema si pose nel momento in cui, una volta convolati a nozze, ci rendemmo conto che stipare le cose di entrambi nella sua casetta di single era un’operazione tutt’altro che banale. Nella consapevolezza che sfruttare al meglio lo spazio era condizione indispensabile alla nostra sopravvivenza, non solo come coppia, decidemmo come prima cosa di dotarci di un letto contenitore.
Mi stavo preparando a cimentarmi nell’impresa eroica di uscire dal grande magazzino di turno solo col letto, invece che con un carico eccezionale di suppellettili tanto geniali quanto superflue, quando mi accorsi dello sguardo luccicante del mio adorato consorte, in evidente furor creativus.
E già: perché il marito ingegnere, come condizione necessaria (ma forse anche sufficiente) alla sua sopravvivenza, ha l’esclusiva della progettazione di tutto – TUTTO – quello che può servire in casa. Figuriamoci se rinuncia all’occasione di progettare un letto contenitore!
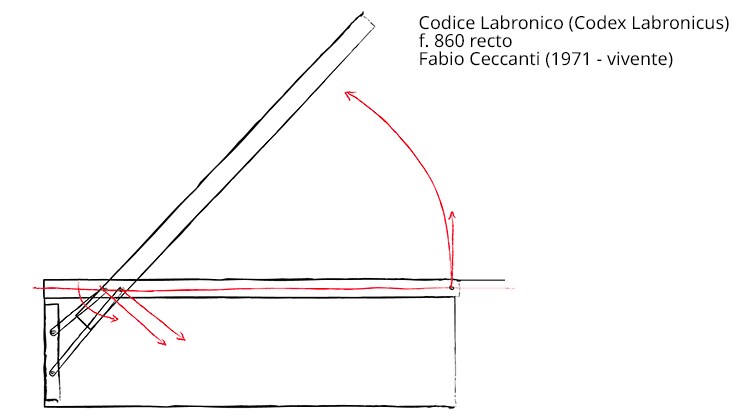
Determinato, si butta anima e corpo nell’impresa, cui sono dedicati i 7342 schizzi raccolti attualmente alle pagine 800 – 1630 di uno dei quaderni che, secondo gli auspici del progettista stesso, passerà alla storia come il Codex labronicus.
Gli schizzi illustrano peraltro con mirabile chiarezza i termini del problema: normalmente un letto è appoggiato contro il muro attraverso la testata. Se, dalla parte della testa, si montasse semplicemente una cerniera tra rete e base del letto, non si potrebbe sollevare il materasso perché la testata andrebbe a sbattere contro il muro. Bisogna quindi sollevare la rete tramite un meccanismo che consenta di muoverla verso l’alto e allo stesso tempo in avanti, ma mai indietro. E qui casca l’asino.
Intermezzo: perché vi racconto i fatti miei?!
Il titolo di questo intervento è “Matematica e Design”. In effetti, avete letto di fedi turche e nastro di Moebius, con il conseguente accenno alla matematica soggiacente. Vi è stato inoltre proposto il problema della realizzazione del meccanismo (matematica) alla base di un letto contenitore (design). Tuttavia, l’enfasi maggiore sembra dedicata, più che agli ingredienti matematico/architetturali, al plot della storia che stiamo raccontando, ovvero alle vicissitudini di una coppia alle prese, oltre che con gli oggetti descritti, con una serie di episodi tragicomici.
Inserire il contenuto tecnico in una narrazione è una vera e propria scelta di campo: come già affermava Bruner, nel lontano 1980, le narrazioni rappresentano infatti un vero e proprio schema cognitivo fondamentale dei nostri processi cerebrali. Di conseguenza, ambientare un argomento “tecnico” in uno sfondo “narrativo” è un espediente comunicativo potenzialmente molto efficace. Stimolando infatti il coinvolgimento emotivo, divertendo, stupendo e spiazzando, lo storytelling predispone il lettore (o l’ascoltatore) all’apprendimento, nella consapevolezza che c’è un profondo legame tra il piano emotivo e quello cognitivo: citando un intervento del collega Stefano Giacovelli, dall’evocativo titolo Recupero emotivo in matematica, per insegnanti di area scientifica, «il benessere del sistema cognitivo permette alle emozioni di avere una dimensione più giusta, mentre il benessere del sistema emotivo permette al sistema cognitivo di "volare"».
In particolare, quello che avete visto nel paragrafo precedente è un tipo di narrazione che possiamo chiamare autofiction: chi scrive prende spunto da proprie esperienze personali (vere o verosimili), facendosi protagonista del plot narrativo che contorna la veicolazione del contenuto matematico. Inserire elementi di autofiction da parte del divulgatore scientifico ha un impatto (potenzialmente) ancora più alto di quello di una narrazione più generica, in virtù della presa emotiva ancor più efficace – specie, in questo caso, nei soggetti mogli (o mariti) di ingegneri, che non possono che condividere il tragicomico destino del narratore. Ovviamente, come tutte le tecniche di comunicazione, anche questa non è scevra da rischi: è facile infatti perdere uno sguardo obiettivo e bisogna prestare la massima attenzione per non farsi stereotipo e, soprattutto, per evitare di occupare eccessivamente la scena – cosa che, nel caso specifico, avendo a disposizione una fonte pressoché inesauribile di aneddoti, incarnata nel corpo e nel ricordo dell’ex marito, è compito particolarmente improbo.
Con questa consapevolezza, quindi, passiamo finalmente al vero e proprio contenuto tecnico che la nostra storia ci ha consentito di introdurre.
Adesso sì: matematica e design
Il componente fondamentale di qualunque letto contenitore è il meccanismo di sollevamento che potete ben vedere sia nell’immagine che nello schizzo del novello Leonardo: un sistema di aste incernierate che ne determina la funzionalità e ne caratterizza il design.

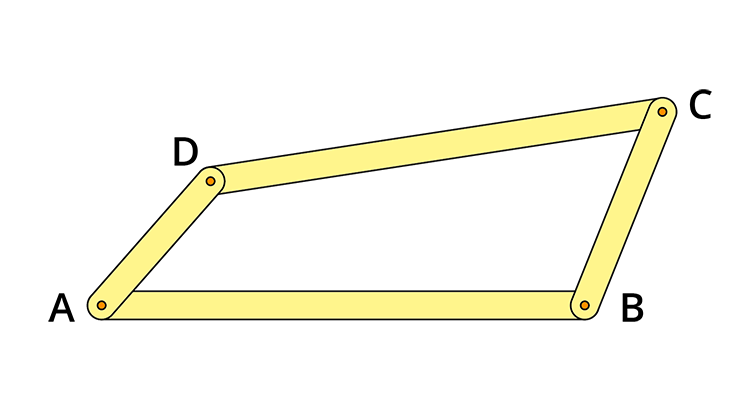
Si tratta di una semplice applicazione del cosiddetto quadrilatero articolato, meccanismo che come dice il nome consiste di quattro aste incernierate, di lunghezza variabile a seconda del comportamento richiesto. Generalmente i quadrilateri articolati che vengono utilizzati negli oggetti di uso comune sono quadrilateri di Grashof, in cui la somma delle lunghezze dell’asta più corta e di quella più lunga è minore o uguale alla somma delle lunghezze delle altre due aste.
Immaginiamo di fissare il lato AB: osserviamo che il movimento di una sola delle altre aste determina quello delle rimanenti, generando fenomeni molto diversi a seconda della lunghezza relativa delle aste.
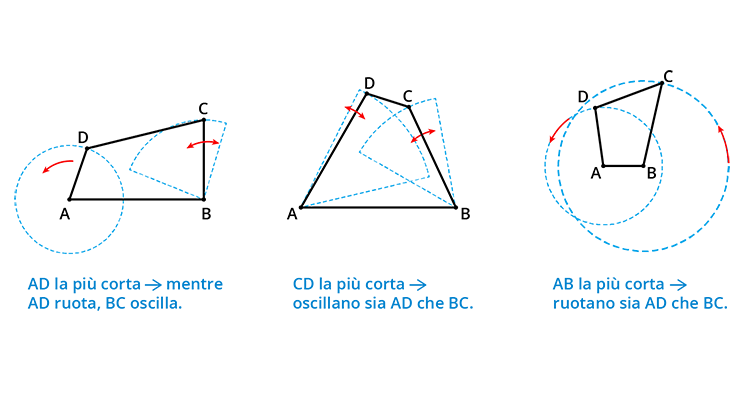
Supponiamo per esempio che l’asta AD sia la più corta: se la facciamo ruotare in senso antiorario anche l’asta BC comincerà a sua volta a girare nello stesso verso. A un certo punto, però, BC invertirà la direzione: mentre AD ruota, BC oscilla. Di conseguenza, un quadrilatero di questo tipo è utile quando si voglia trasformare un moto circolare in un moto oscillatorio, o viceversa, come succede nella bicicletta, quando la coscia oscilla e la pedivella gira. Supponiamo ora che l’asta più corta sia CD: in questo caso l’asta AD non riuscirà a compiere una rotazione completa, quindi oscilleranno sia AD sia BC. Infine, se l’asta più corta è AB, come accade facendo ruotare AD anche CB si muove nello stesso modo.
Questo semplice meccanismo è alla base del funzionamento di innumerevoli oggetti di uso più o meno comune: la già menzionata bicicletta, il pedale delle vecchie macchine da cucire, il pantografo, le bilance, le tende alla veneziana, certe lampade da tavolo (note infatti come lampade a pantografo), i sollevatori per l’ispezione dei lampioni stradali, le sospensioni degli autoveicoli, lo sterzo degli stessi. E il letto contenitore, naturalmente!
Fate un salto dal ferramenta a comprare staffe di acciaio di diversa lunghezza, forate, e qualche bel bullone, con le quali provare con i vostri studenti a riprodurre tutti i meccanismi menzionati qui sopra. Giocare a fare Leonardo li appassionerà di certo e, en passant, è probabile che imparino più matematica che nel corso dell’ennesima lezione frontale. Lezione che, naturalmente, sarà poi molto utile per raccogliere le idee, dopo che l’attività laboratoriale avrà stimolato l’interesse e, auspicabilmente, la necessità della formalizzazione e del rigore.
Epilogo
Naturalmente il letto contenitore a casa Ceccanti non ha mai visto la luce. Nel frattempo, il marito è stato sostitituito dal cane, con piena soddisfazione di tutte le parti coinvolte. Come contenitore, approfittando dell’assenza del maniaco (dell’ordine, cosa avete capito!), mi limito a utilizzare la parte sottostante alla rete, che stipo all’inverosimile di scatoline scatolone e scatolette, a loro volta stipate all’inverosimile di maglie scarpe lenzuola e chi più ne ha più ne metta.
Post scriptum
Nell’intermezzo abbiamo parlato di tecniche di comunicazione e di assi nella manica di divulgatori scientifici. Voi che ci leggete, in quanto insegnanti, avete un compito diverso. C’è infatti una differenza sostanziale tra le finalità della comunicazione e quelle della didattica: la didattica si propone di "insegnare", mentre la comunicazione ambisce a "incuriosire", "demistificare", "intrattenere", "divertire", in modo da creare terreno fertile a un futuro apprendimento, che può avvenire in contesti e con tempi diversi. Tuttavia, anche nella didattica è importante la dimensione ricreativa ed emotiva, così come peraltro una buona comunicazione deve anche informare.
Un insegnante che non motivi e incuriosisca i suoi studenti ha poca possibilità di essere ascoltato, quando passa alla formalizzazione. La matematica di cui i nostri studenti hanno esperienza quotidiana è infatti oggettivamente poco affascinante; inoltre, impadronirsi del linguaggio e della simbologia che la caratterizzano richiede innegabilmente un certo sacrificio. Difficile, quindi, pretendere che affrontino questa fatica, se non sono adeguatamente motivati a farlo. Questo è in fondo il più importante compito di un insegnante: rispondere alla domanda "a cosa serve saper risolvere le equazioni di secondo grado?" PRIMA di passare alla formula per farlo.
Molti docenti rispondono che non c'è tempo, ma è un errore di valutazione: ragazzi adeguatamente motivati saranno molto più attenti nel momento della spiegazione, affronteranno più volentieri l'imprescindibile training necessario a impadronirsi delle tecniche di calcolo e si riveleranno in definitiva non solo molto più ricettivi, ma anche più veloci, perché avranno fretta di capire, mossi dalla curiosità.
Un docente che motiva e incuriosisce, inoltre, guadagna sul campo la stima, il rispetto e addirittura l'affetto dei suoi studenti, cosa non affatto scontata a priori. Un docente che stimoli i suoi studenti, servendosi di tutti i trucchi, tra cui quelli cui abbiamo accennato in questo articolo, può trasmettere loro quanto la sua materia possa essere una bellissima scoperta intellettuale e un'affascinante esperienza culturale: avendone compreso la bellezza, la fatica che comporta troverà una sua giustificazione, nell'attesa della gratificazione di padroneggiarne tecniche e risultati.